목차
제조 회사에서 six-sigma를 업무에 적용하는 경우가 많이 있습니다. 그중에서 공정능력을 의미하는 Cp(Capability of Process)와 공정능력지표를 의미하는 Cpk(Capabiliry of Process Index)에 대한 이해는 업무에 많은 도움이 될 수 있습니다. 관련된 내용을 정리해 봅니다.
Cp : Capability of Process (공정능력)
Cp는 제조 공정의 분포의 폭을 나타내는 지표입니다. 일반적인 제조 현장의 품질 데이터는 정규 분포를 기반으로 한다고 가정합니다. 다음의 계산식을 보고 좀 더 설명해 보겠습니다.
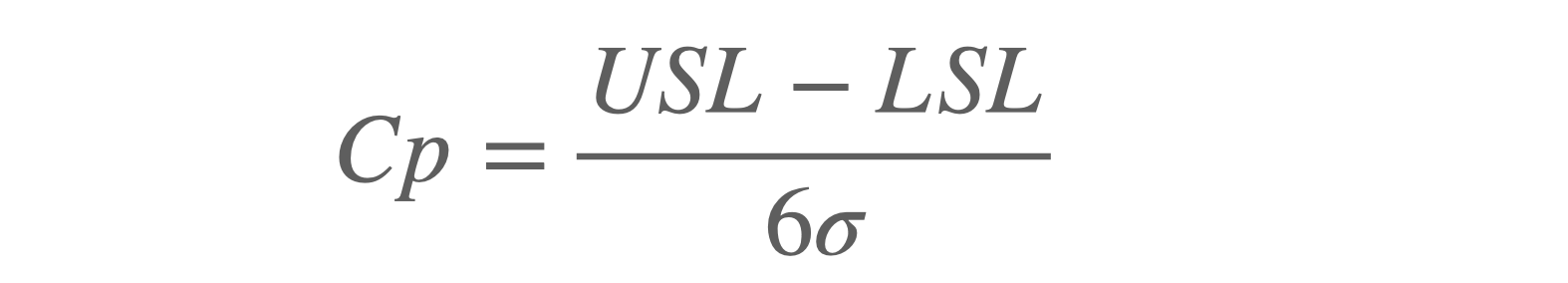
공정능력(Cp)을 계산할 때 총 3개의 값이 필요합니다. USL과 LSL 그리고 분모에 있는 시그마의 값입니다.
USL(Upper Spec Limit)과 LSL(Lower Spec Limit)은 관리 스펙 상한과 관리 스펙 하한이라 하며, 만들어지는 제품의 규격 범위입니다. 즉, 제품의 사양입니다. 제품의 관리값이 이 사양 내에 있어야 양품이 되는 겁니다. 두 값은 설비에서 만들어지는 것이 아니라 양품 조건이 되는 겁니다.
시그마는 설비가 만들어 내는 값입니다. 제품의 양품 기준 값에 대한 통계적 수치를 말합니다.
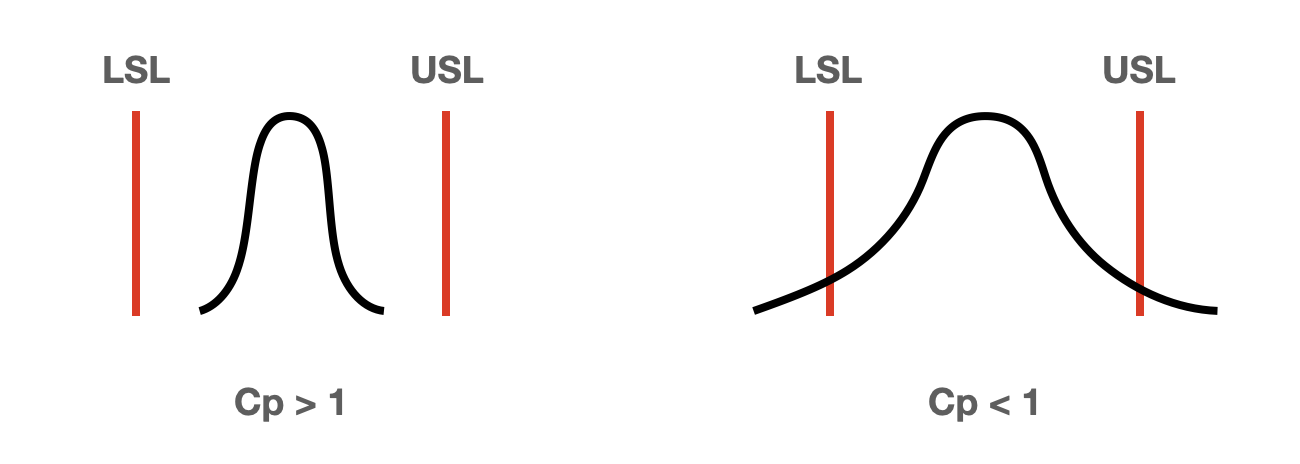
공정능력(Cp)의 물리적 의미는 설비가 제품을 생산할 때 품질 데이터의 변동폭(분모) 이 제품 사양 범위(분자) 보다 얼마나 작은 지를 나타냅니다.
Cpk : Capability of Process Index (공정능력지수)
Cp는 단순하게 품질 데이터의 변동만을 고려합니다. 데이터의 치우침이 발생돼도 Cp의 값은 변화가 없습니다.
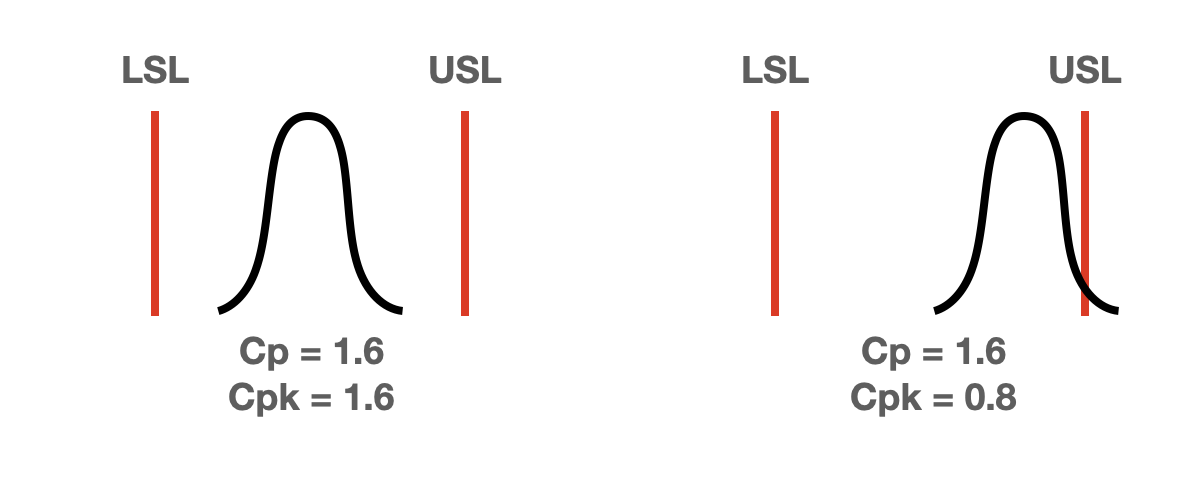
위의 이미지에서 품질데이터의 분포(검은색)는 변하지 않는다는 가정에서 관리 상한에 데이터가 몰렸다고 하면 Cp의 변화는 없지만 Cpk가 달라지는 것을 알 수 있습니다.
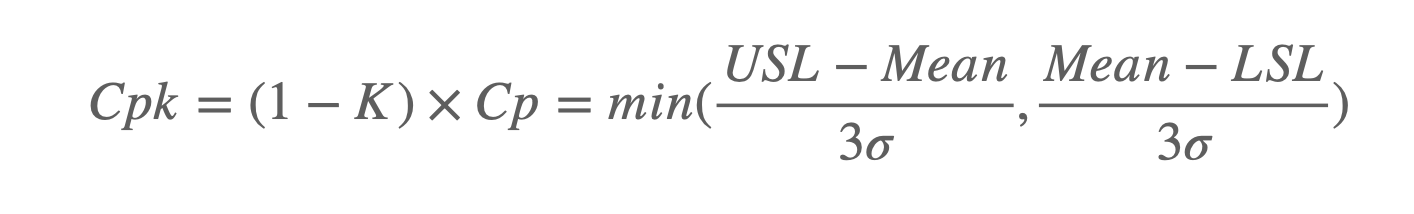
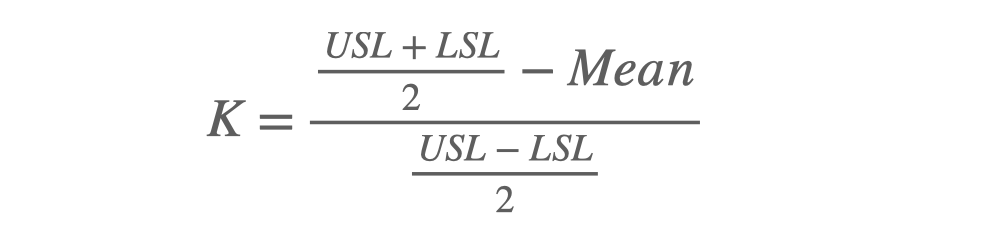
정규분포를 갖는 품질데이터 생성하기(파이썬 코드)
공정능력을 이해하기 위해 파이썬을 이용하여 품질데이터를 생성하고 각각의 Cp와 Cpk를 구하는 함수를 정의해 보겠습니다.
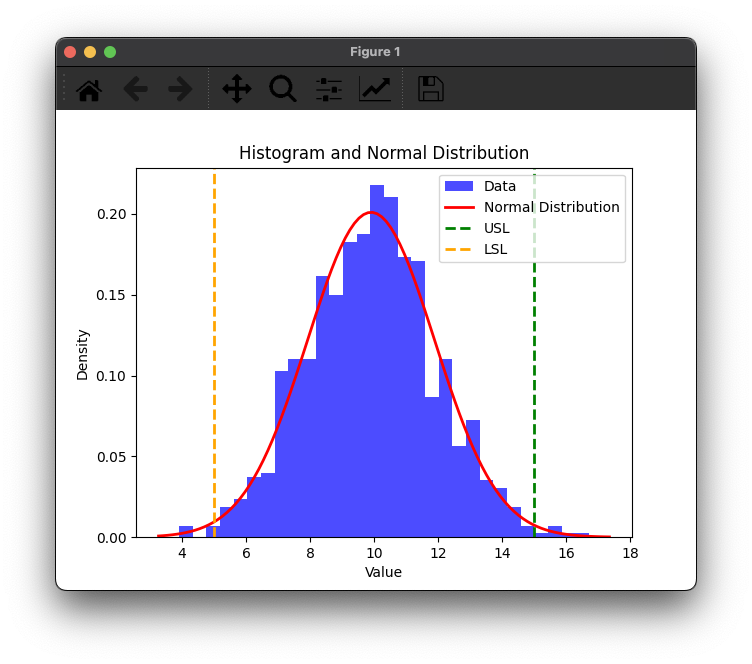
우선 정규분포를 갖는 데이터셋을 만드는 코드를 작성합니다.
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# 예제 데이터
data = np.random.normal(loc=10, scale=2, size=1000) # 정규 분포를 따르는 가상의 데이터
# 명세 한계
usl = 15
lsl = 5
# 데이터의 히스토그램
plt.hist(data, bins=30, density=True, alpha=0.7, color='blue', label='Data')
# 정규 분포의 확률 밀도 함수를 그립니다.
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, np.mean(data), np.std(data))
plt.plot(x, p, 'k', linewidth=2, color='red', label='Normal Distribution')
# 명세 한계를 표시합니다.
plt.axvline(usl, color='green', linestyle='dashed', linewidth=2, label='USL')
plt.axvline(lsl, color='orange', linestyle='dashed', linewidth=2, label='LSL')
plt.title('Histogram and Normal Distribution')
plt.xlabel('Value')
plt.ylabel('Density')
plt.legend()
plt.show()
공정능력 및 공정능력지수 함수 정의
공정능력을 평가하기 위해서 총 3개의 데이터가 필요하다고 했습니다. USL과 LSL의 두 개의 값과 품질을 나타내는 데이터군이 필요합니다. 함수에서는 총 3개의 변숫값을 입력받게 했습니다.
함수로 입력된 data에서 공정능력 계산에서 필요한 데이터는 표준편차(시그마)입니다. np.std() 함수를 사용해서 시그마 값을 계산했습니다.
def calculate_cp_cpK(data, usl, lsl):
mean = np.mean(data)
std_dev = np.std(data, ddof=1) # ddof=1 for sample standard deviation
cp = (usl - lsl) / (6 * std_dev)
cpk_upper = (usl - mean) / (3 * std_dev)
cpk_lower = (mean - lsl) / (3 * std_dev)
cpk = min(cpk_upper, cpk_lower)
return cp, cpk
측정시스템의 성능을 Cp, Cpk로 표현이 가능할까?
가끔 현장에서 측정시스템의 성능을 Cp와 Cpk의 수치로 평가하는 경우가 있습니다. 하지만 측정 시스템을 Cpk로 직접 평가하는 것은 일반적으로 적절하지 않습니다. Cpk는 주로 제조 공정의 공정 능력을 측정하는 지표이며, 측정 시스템의 정확성과 일관성을 나타내지 않습니다.
측정 시스템을 평가하기 위해서는 **측정 시스템 분석(MSA, Measurement System Analysis)**을 수행해야 합니다. MSA는 측정 시스템의 정확성, 일관성, 반복성 등을 평가하는 방법론입니다. 주요 MSA 지표로는 Gage R&R (Gage Repeatability and Reproducibility)이 있습니다.
Gage R&R는 측정 시스템의 측정 오차를 측정하고, 해당 측정 시스템이 공정 변동과 어떻게 관련되어 있는지를 이해하는 데 도움이 됩니다. Gage R&R의 결과는 % R&R, 퍼센트 오차, ANOVA 등의 통계적인 지표들을 제공합니다.
마치며
지금까지 공정능력(Cp)과 공정능력지수(Cpk)에 대해 물리적인 의미와 계산식 그리고 파이썬을 이용한 예제를 설명했습니다. 측정시스템의 경우에는 Cp와 Cpk를 사용하는 대신 Gage R&R로 평가를 해야 하며 이에 대해서는 추후 자료를 다시 정리하도록 하겠습니다.

